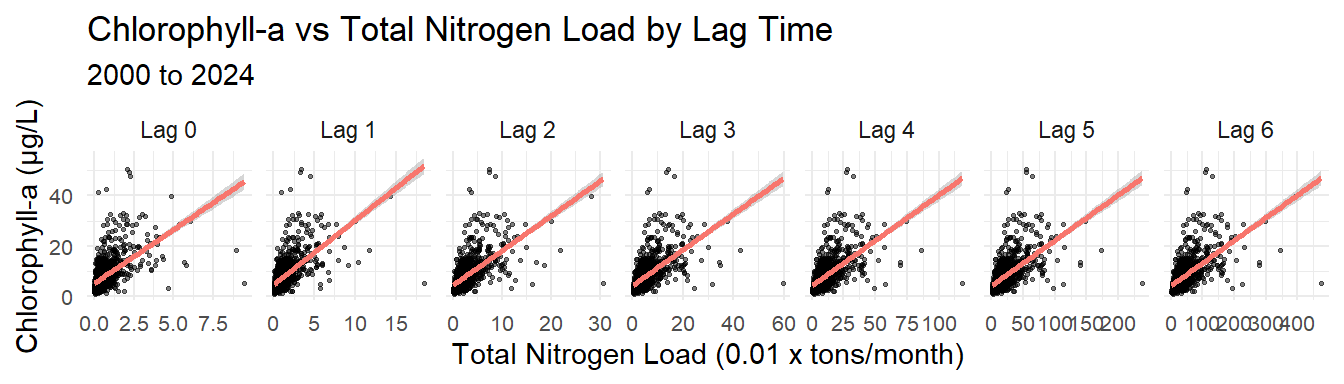
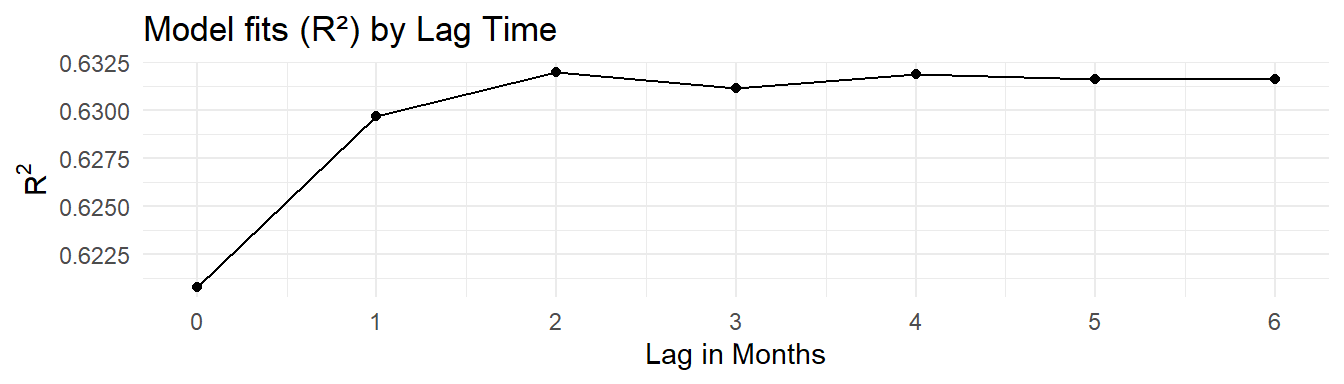
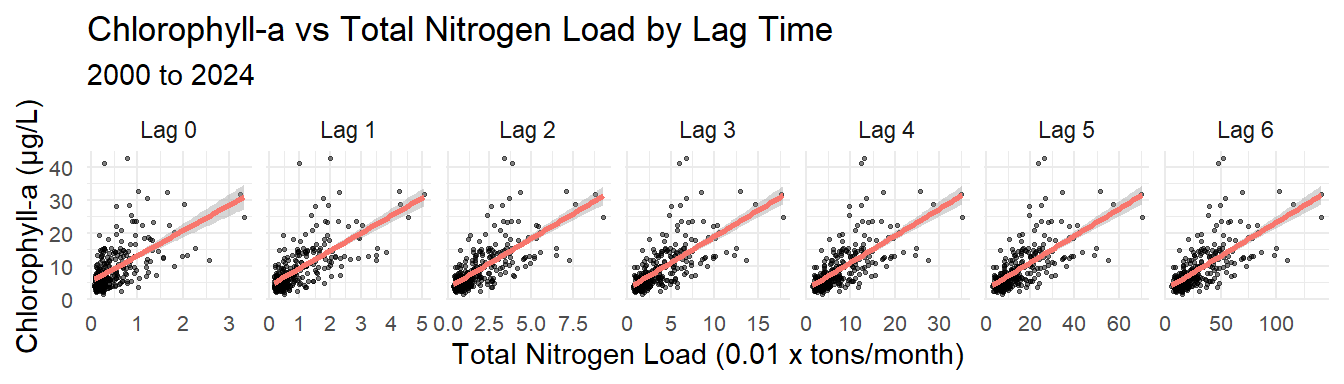
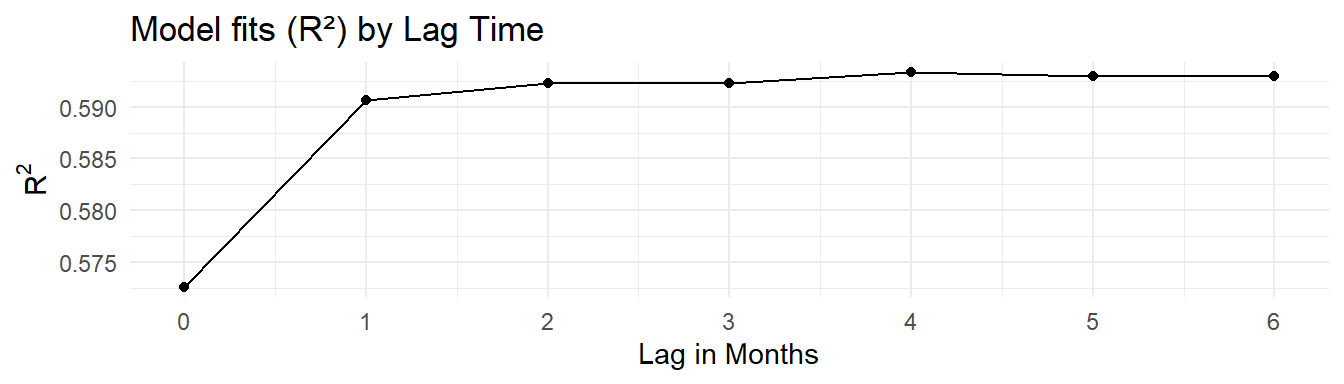
chla ~ factor(bay_segment):factor(mo) + tn_load:factor(bay_segment)Exploring the Assimilative Capacity of Old Tampa Bay
Original Model, All Bay Segments
The cumulative lag model from Janicki and Wade 1996 is specified as:
\[ \text{chla}_{t, s} = \alpha_{t, s} + \beta_s \left( \Sigma_{i = I_0}^{I_n} L_{t - i, s} \right) \]
where \(\text{chla}_{t, s}\) is the chlorophyll-a concentration at month \(t\) and bay segment \(s\), \(\alpha_{t, s}\) is the intercept term that varies by \(t\) and \(s\), \(\beta_s\) is the coefficient for the cumulative load term that varies by \(s\), and \(L_{t - 1, s}\) is the cumulative nitrogen nitrogen load evaluated at different lags from \(I_0\) as the present month in the time series to \(I_n\) months for each \(s\).
Models are created with the following linear model structure in R, where the tn_load variable is the cumulative lag load for different \(n\) lags.
OTB Only Model
The models are the same as above except the bay segment term is removed since only OTB is being modeled.
The cumulative lag model from is specified as:
\[ \text{chla}_{t} = \alpha_{t} + \beta \left( \Sigma_{i = I_0}^{I_n} L_{t - i} \right) \]
where \(\text{chla}_{t}\) is the chlorophyll-a concentration at month \(t\), \(\alpha_{t}\) is the intercept term that varies by \(t\), \(\beta\) is the coefficient for the cumulative load term, and \(L_{t - i}\) is the cumulative nitrogen load evaluated at different lags from \(I_0\) for the present month to \(I_n\) months.
Models are run with the following linear model structure in R, where the tn_load variable is the cumulative lag load for different \(n\) lags.
chla ~ factor(mo) + tn_loadAssimilative Capacity Analysis
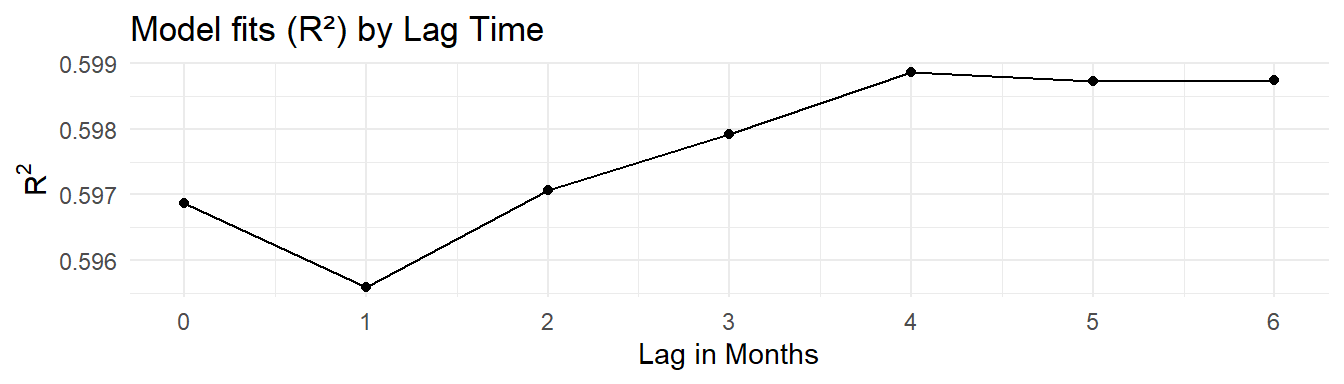
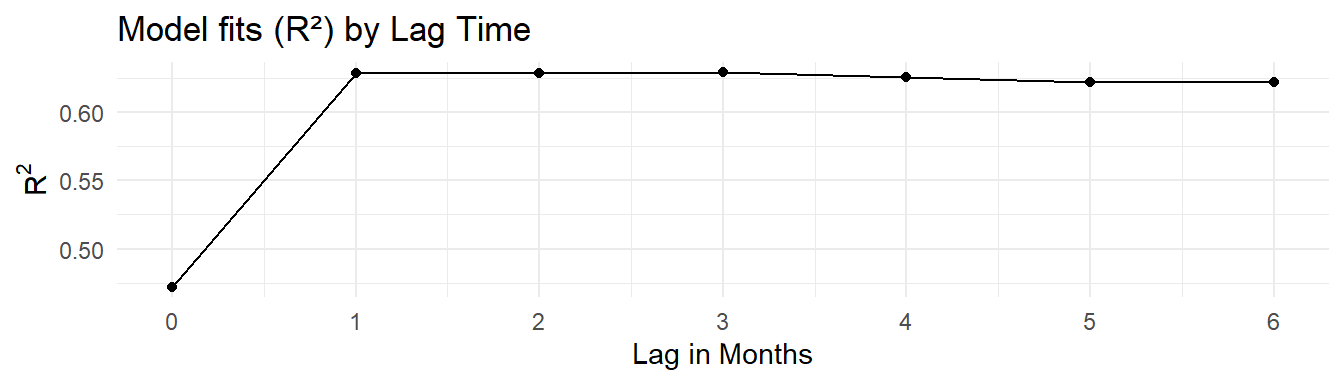
The cumulative lag model with a 3-month lag was chosen for the assimilative capacity analysis based on the results above and previous work by Janicki and Wade (1996).
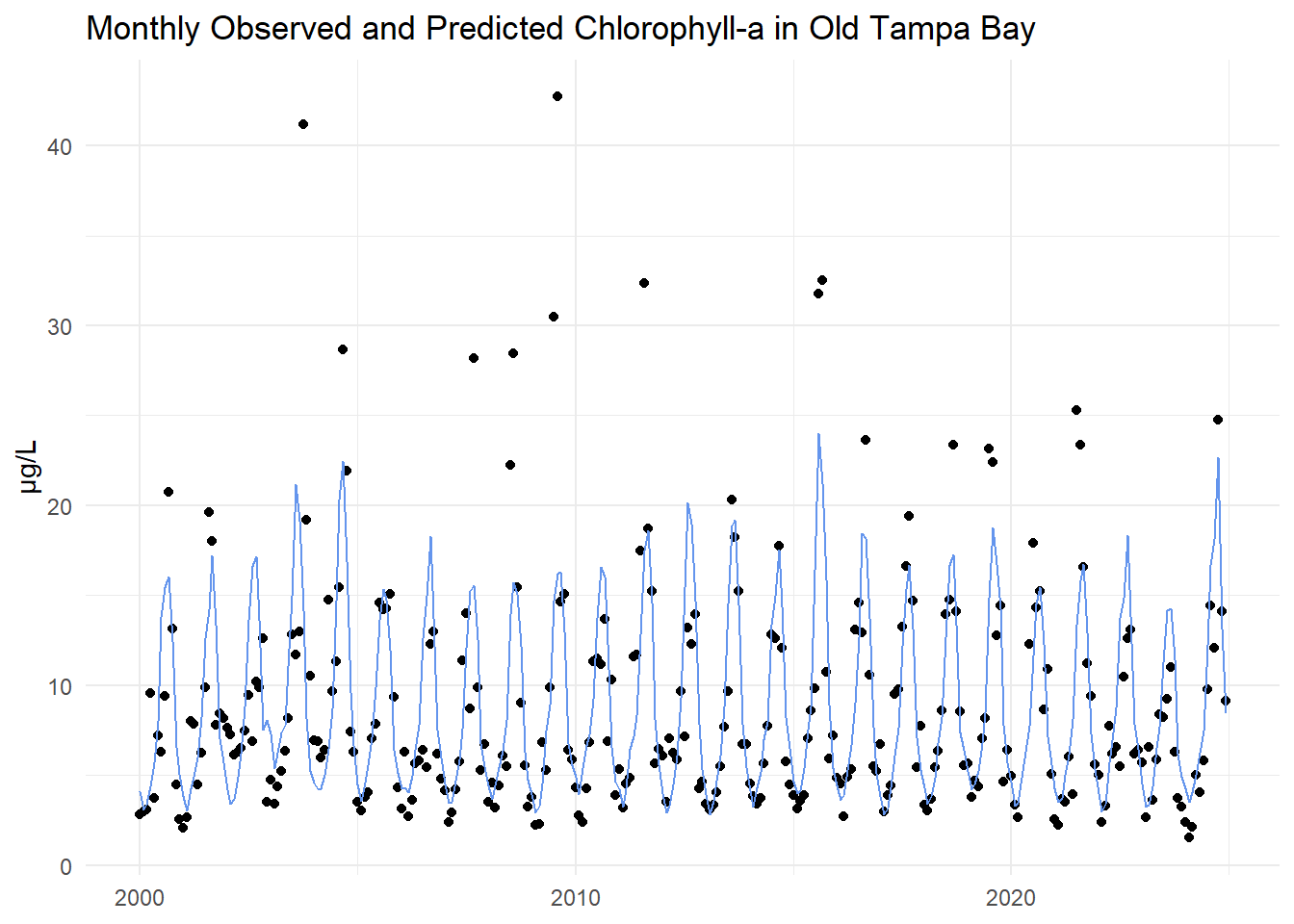
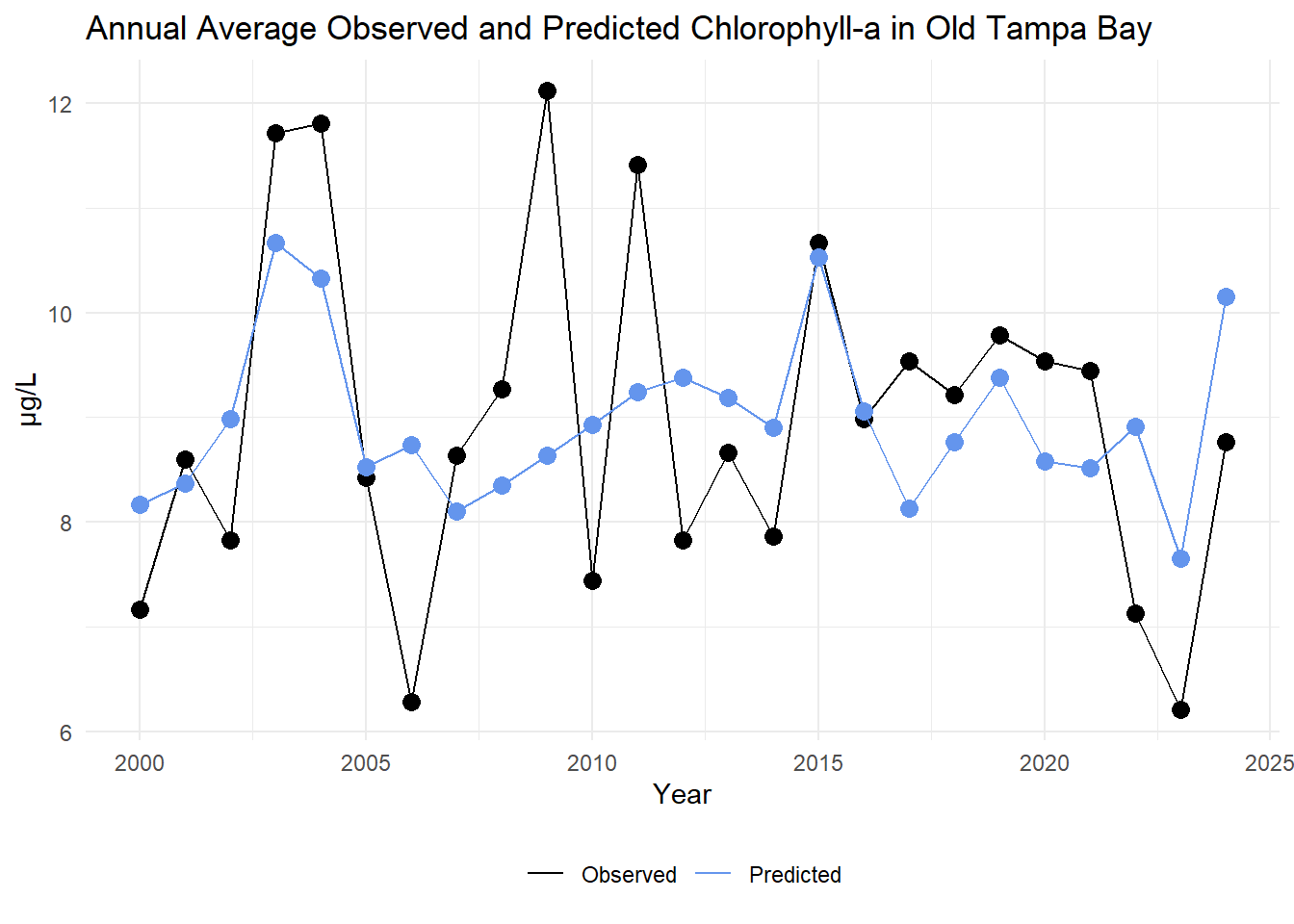
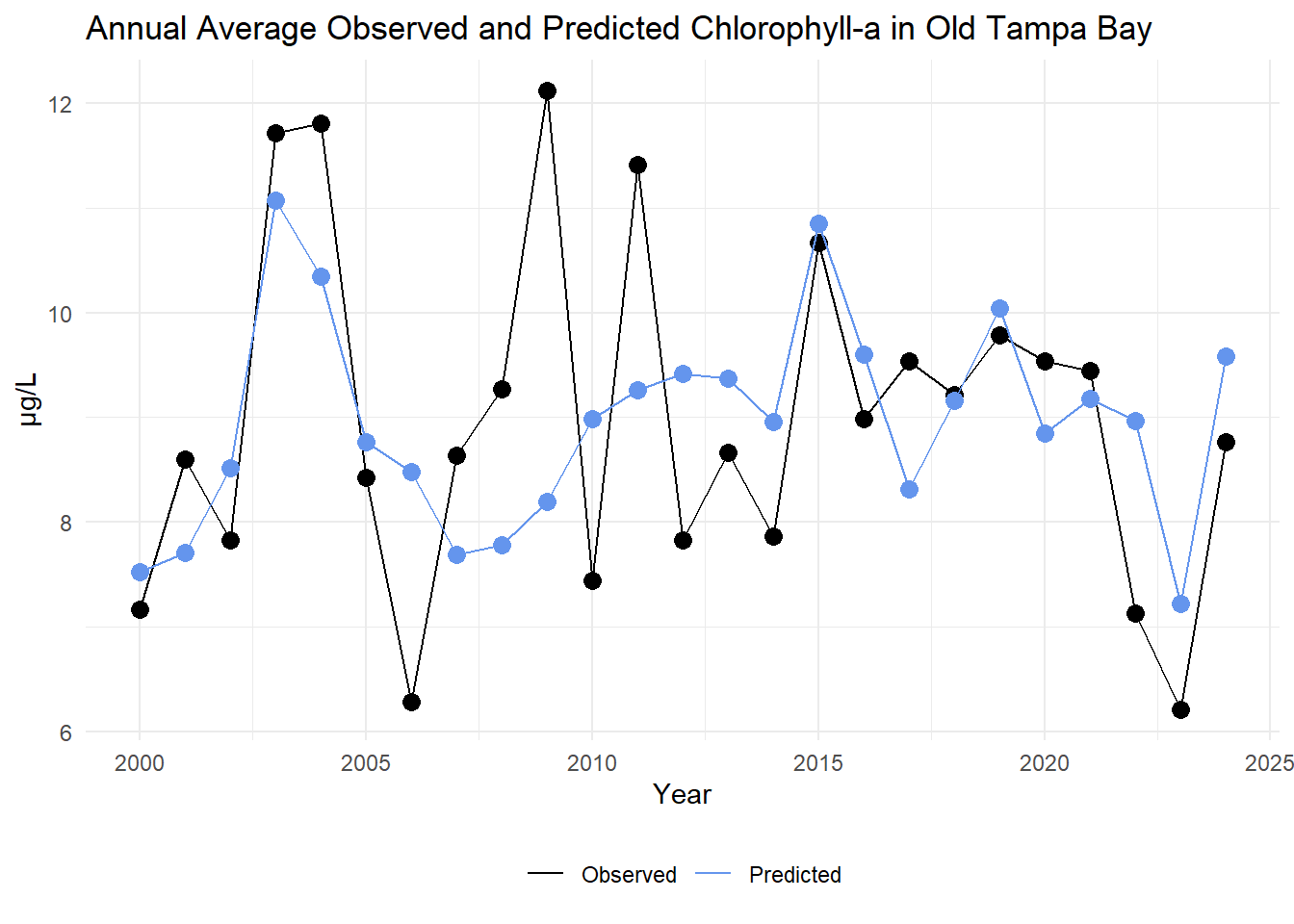
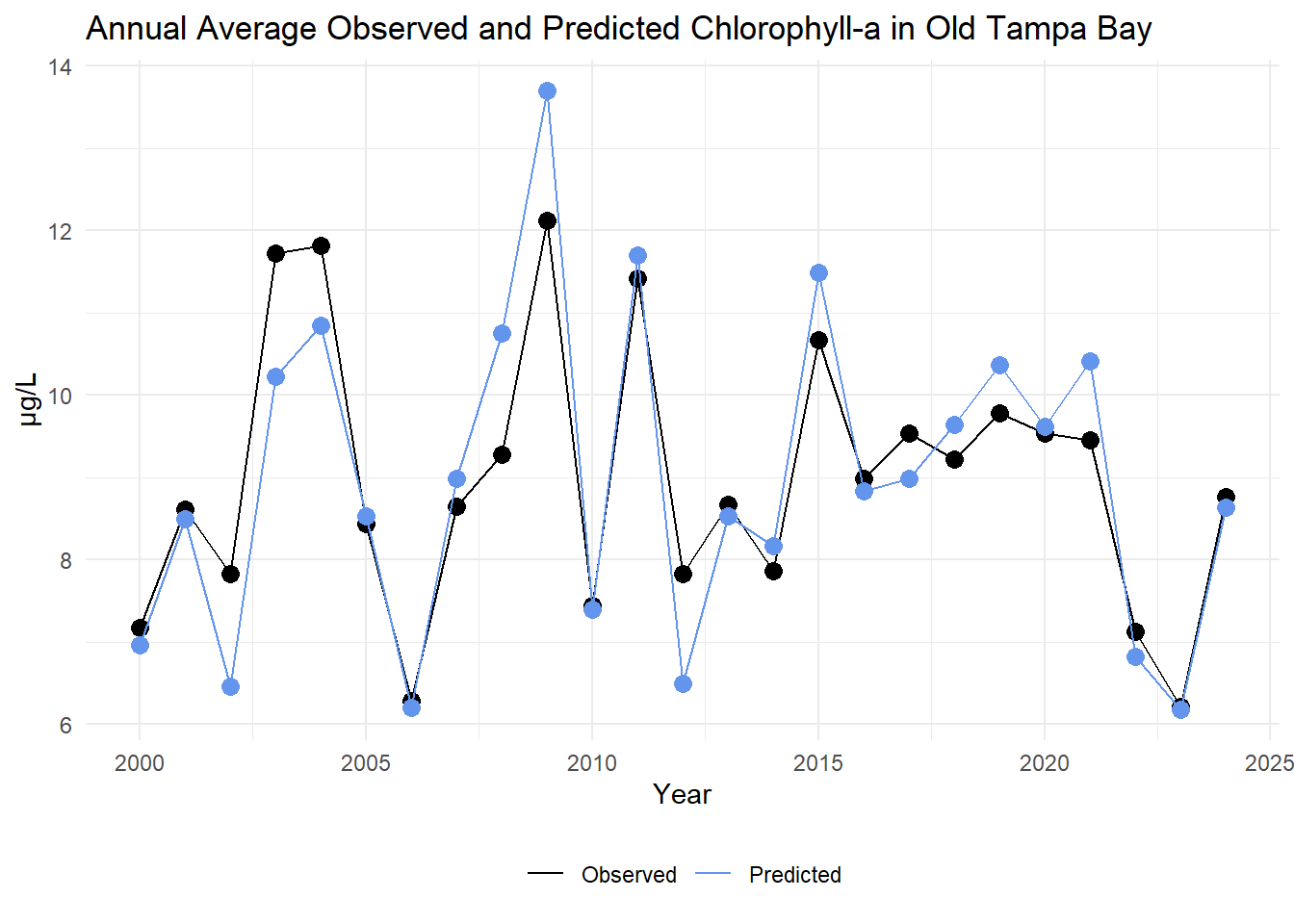
The annual average observed and predicted chlorophyll-a concentrations are compared for Old Tampa Bay below.
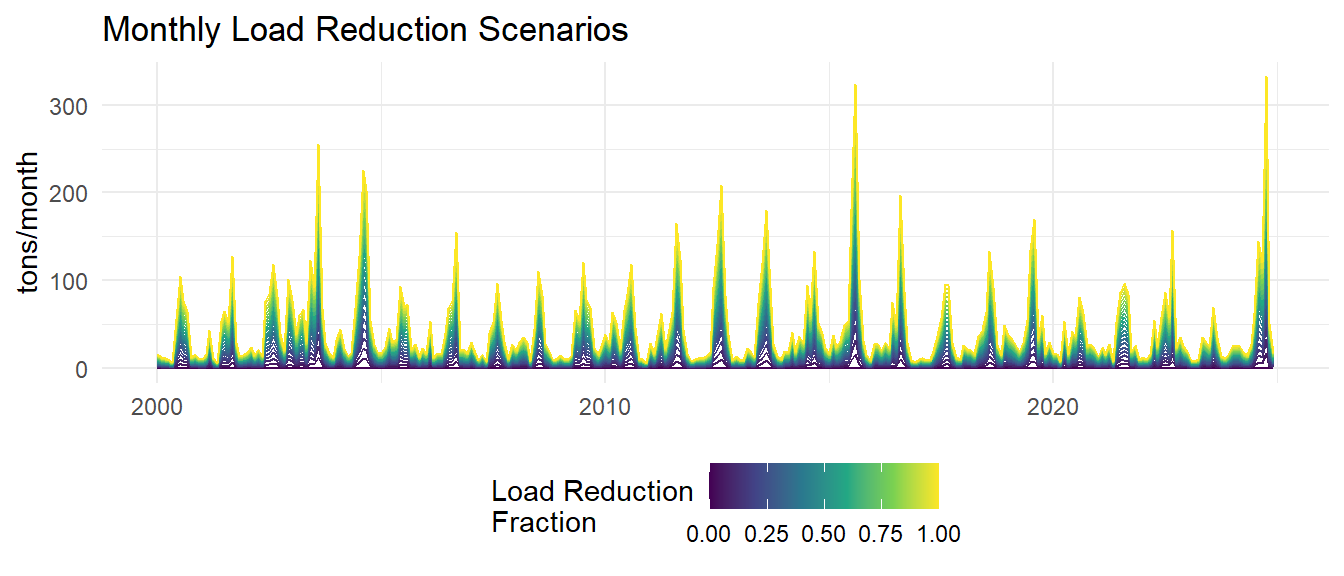
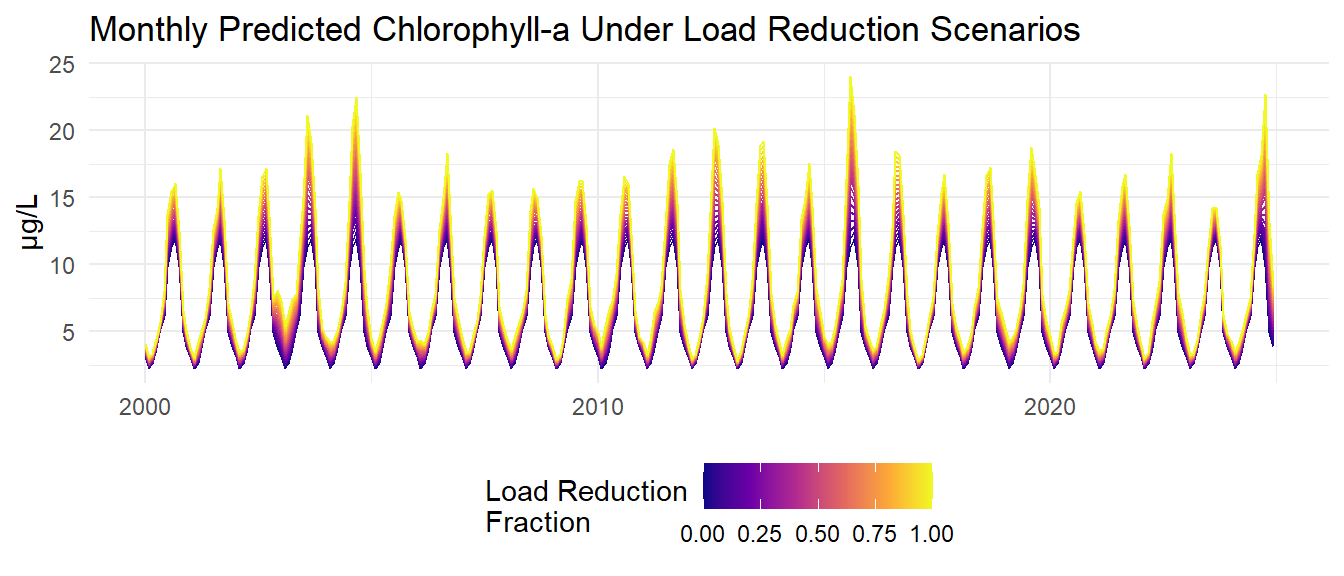
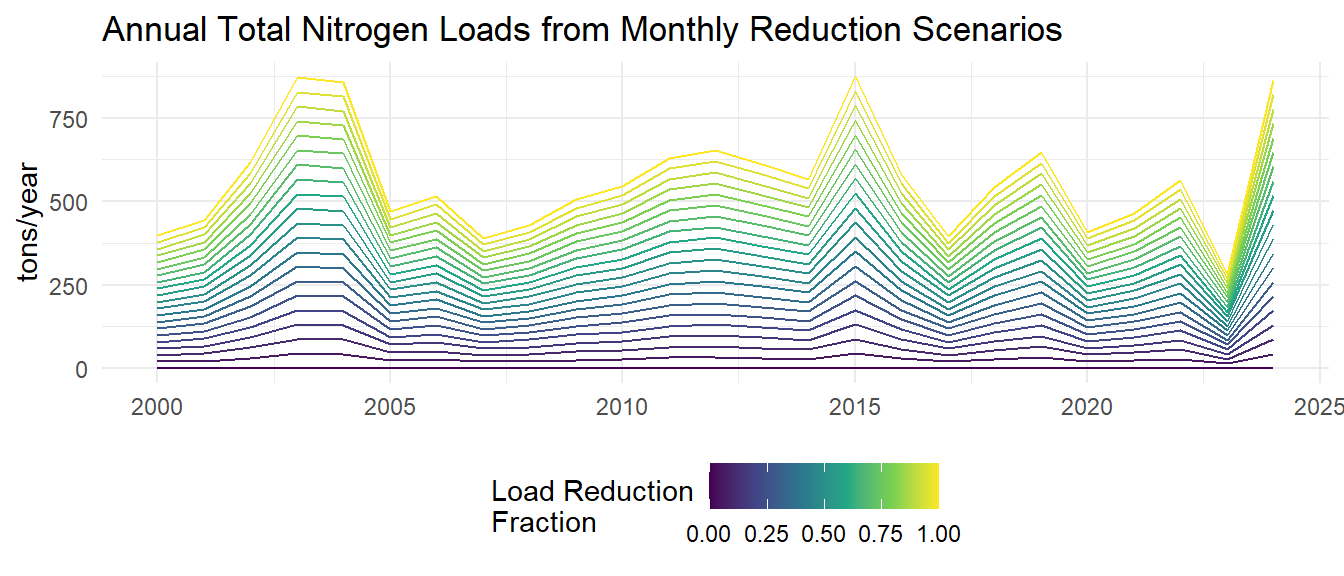
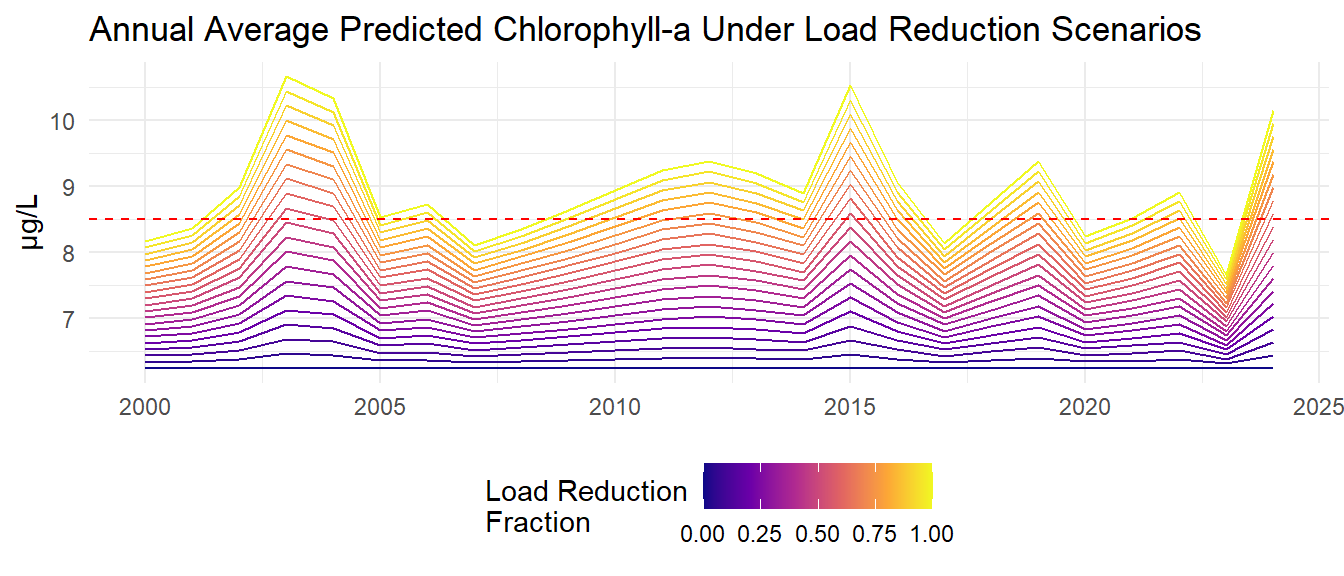
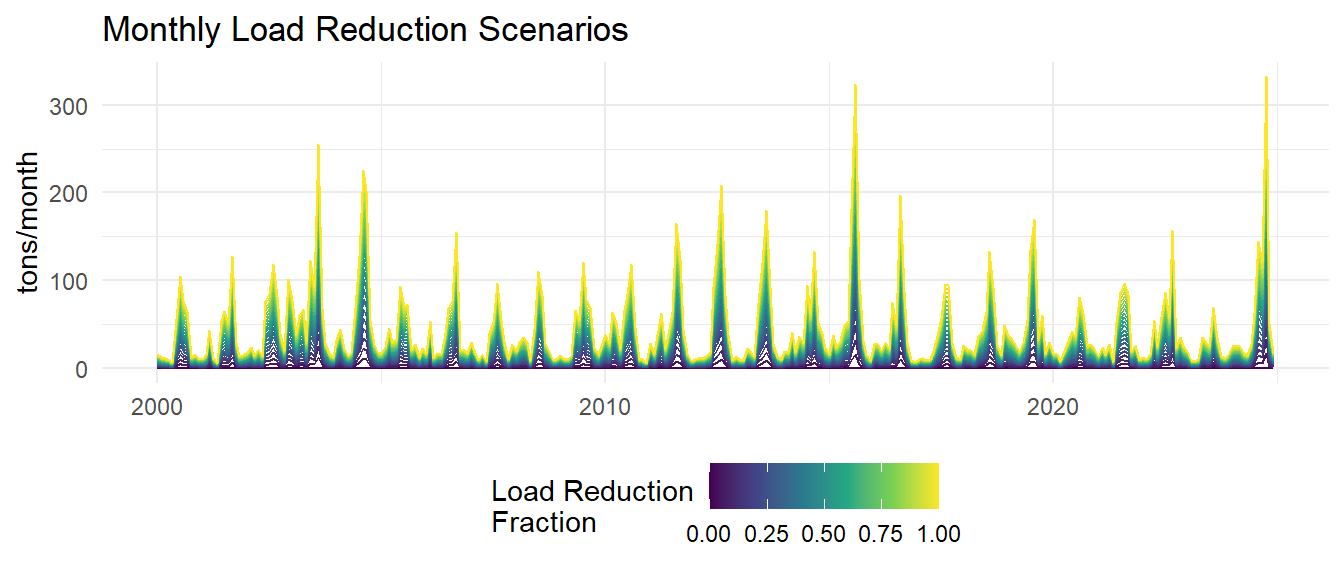
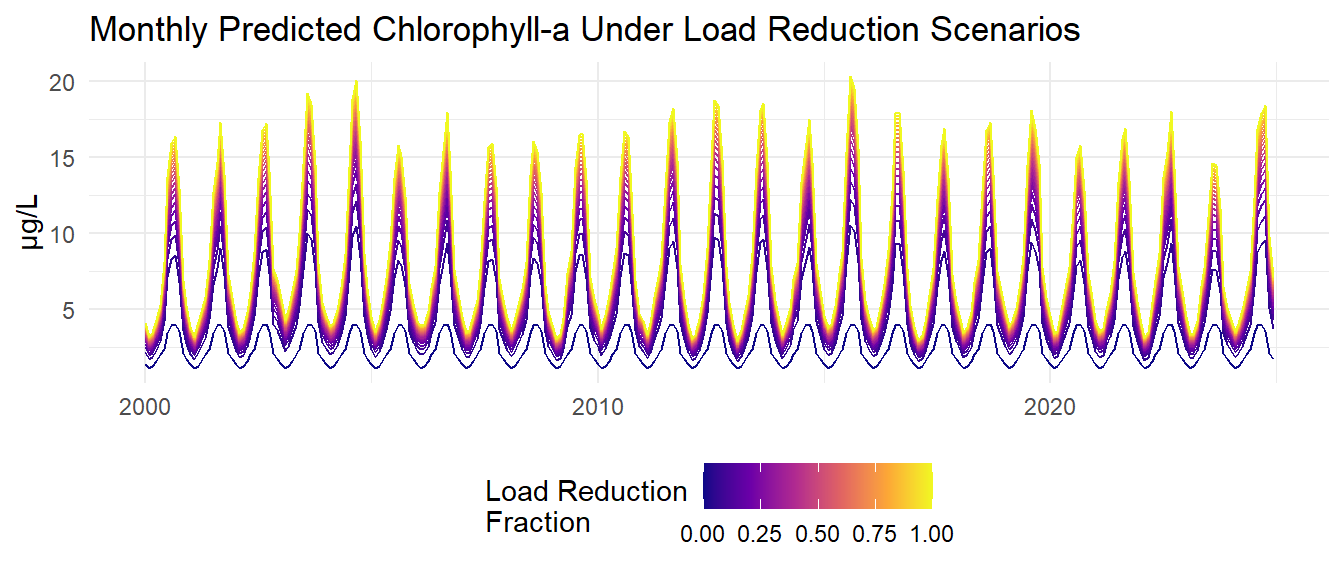
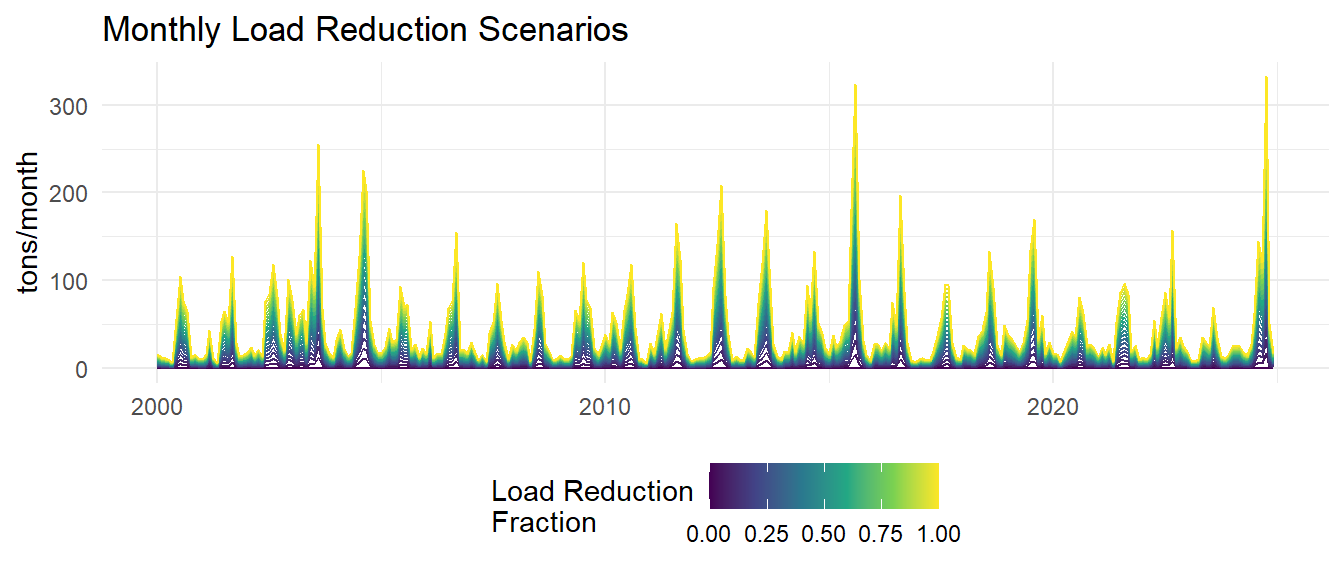
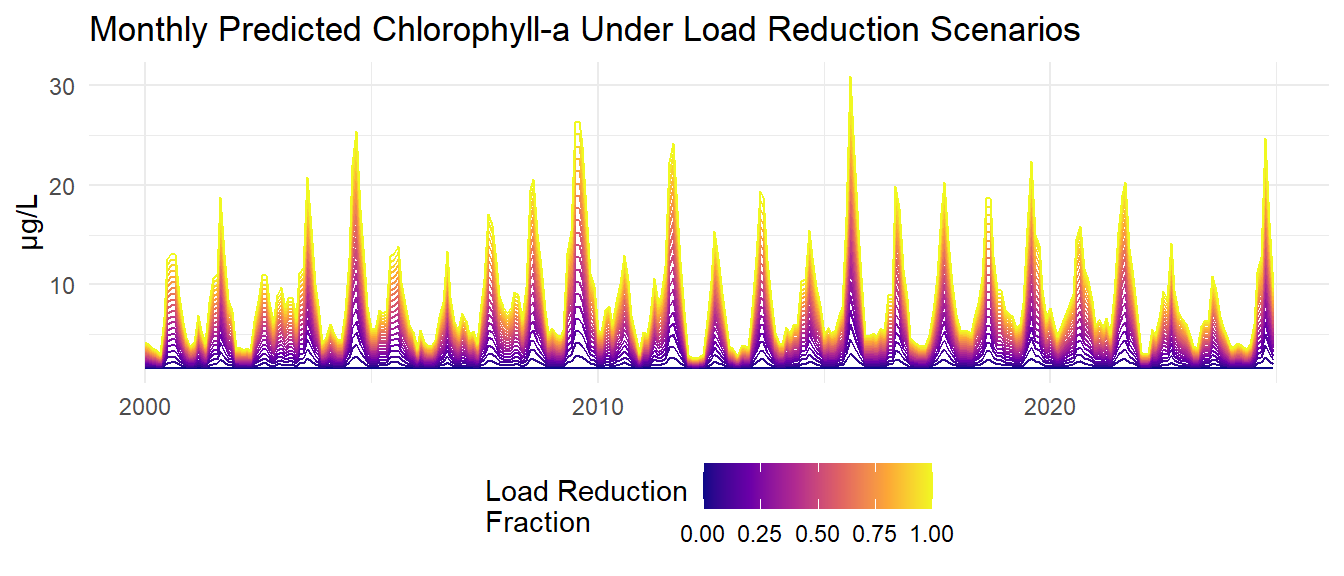
The assimilative capacity analysis involves simulating various nitrogen load reduction scenarios and predicting the resulting chlorophyll-a concentrations using the developed models. Monthly loads are reduced by fractions ranging from 0% to 100% in 5% increments. The models are then used to predict chlorophyll-a concentrations under each load reduction scenario.
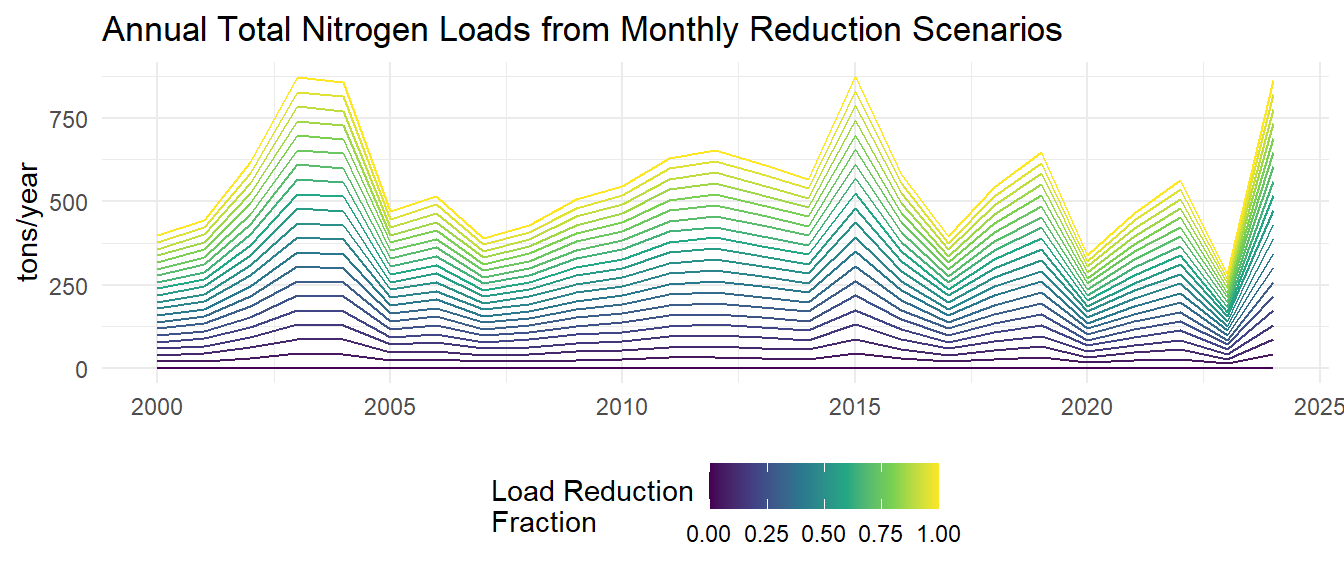
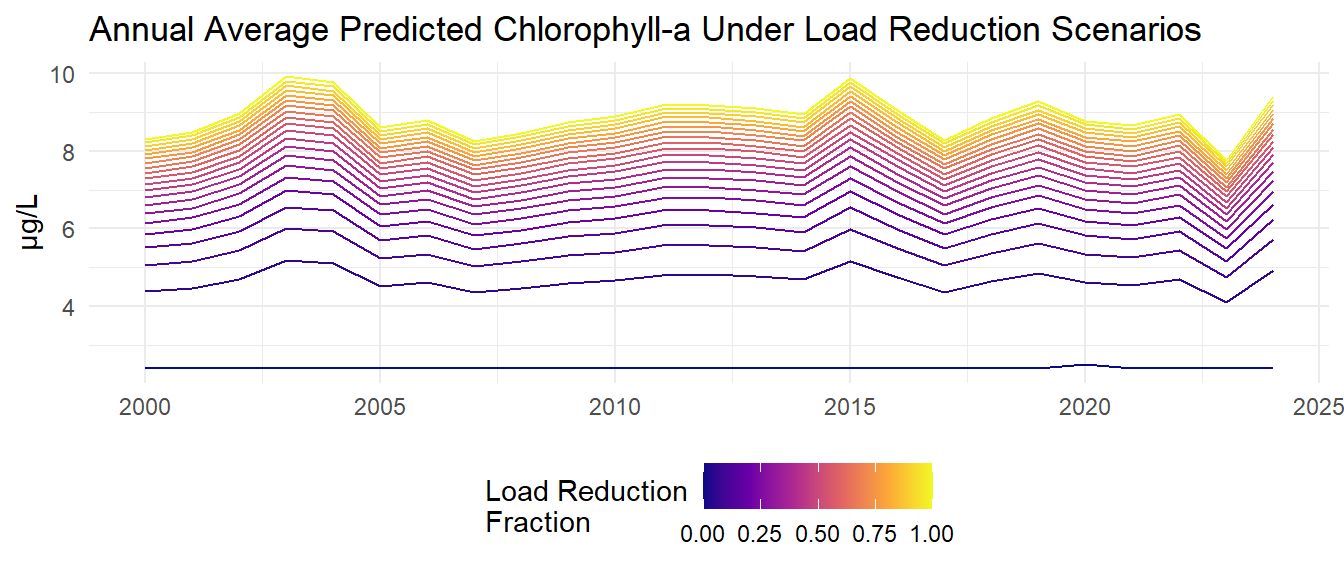
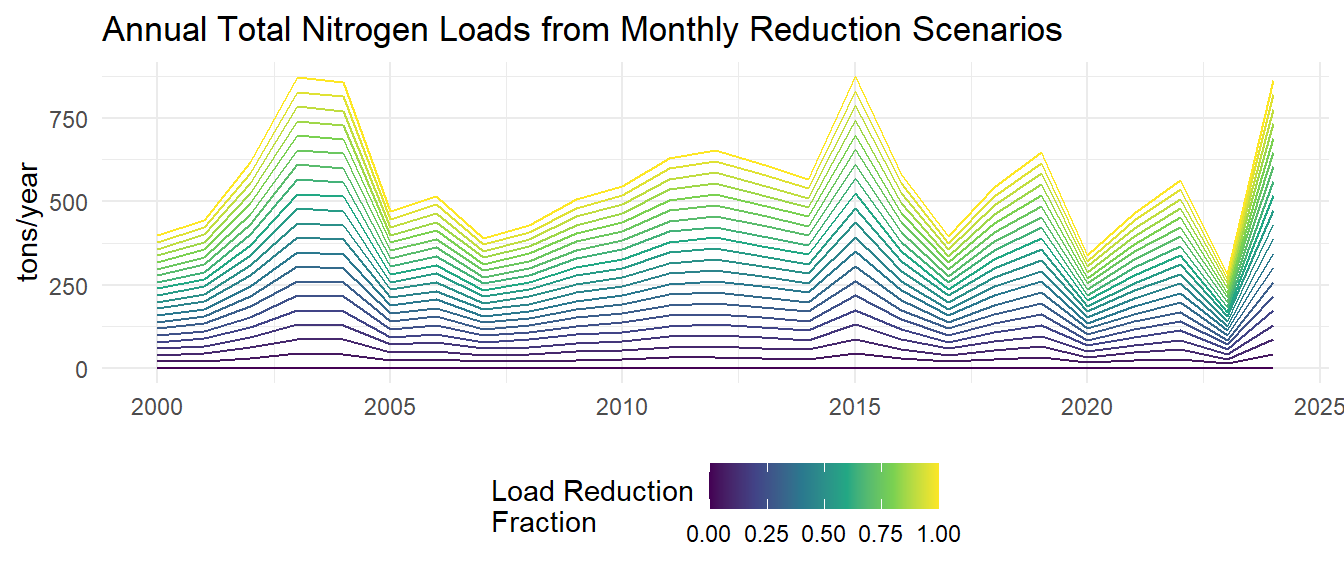
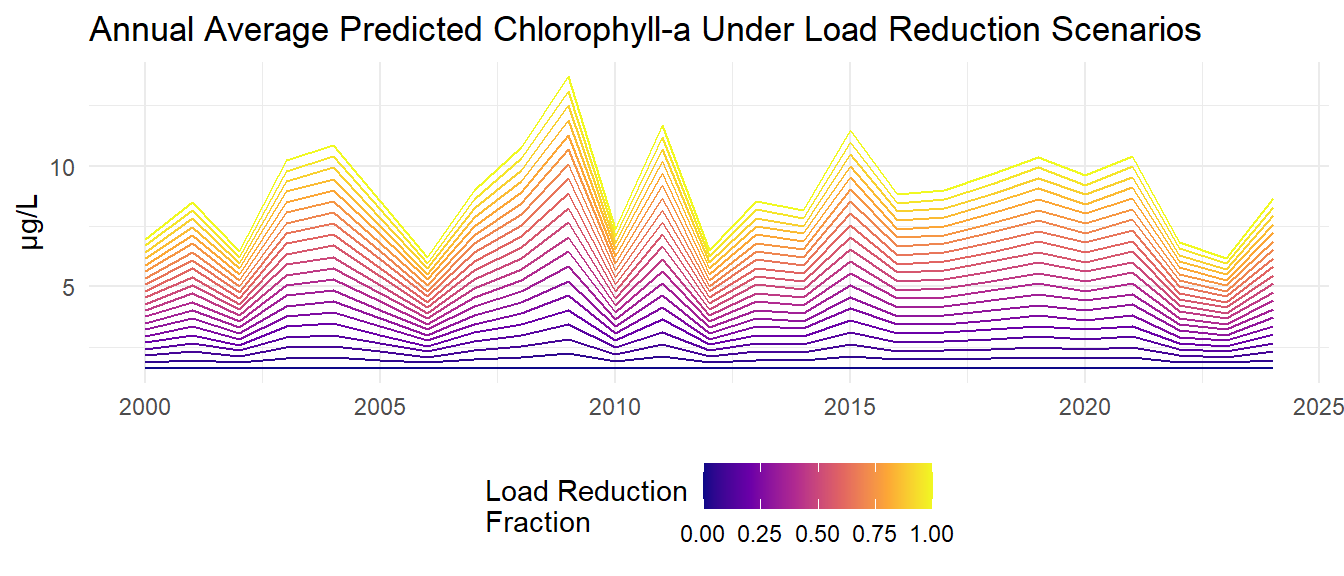
Monthly model predictions are then aggregated to annual average predicted chlorophyll-a and total nitrogen loads for each load reduction scenario.
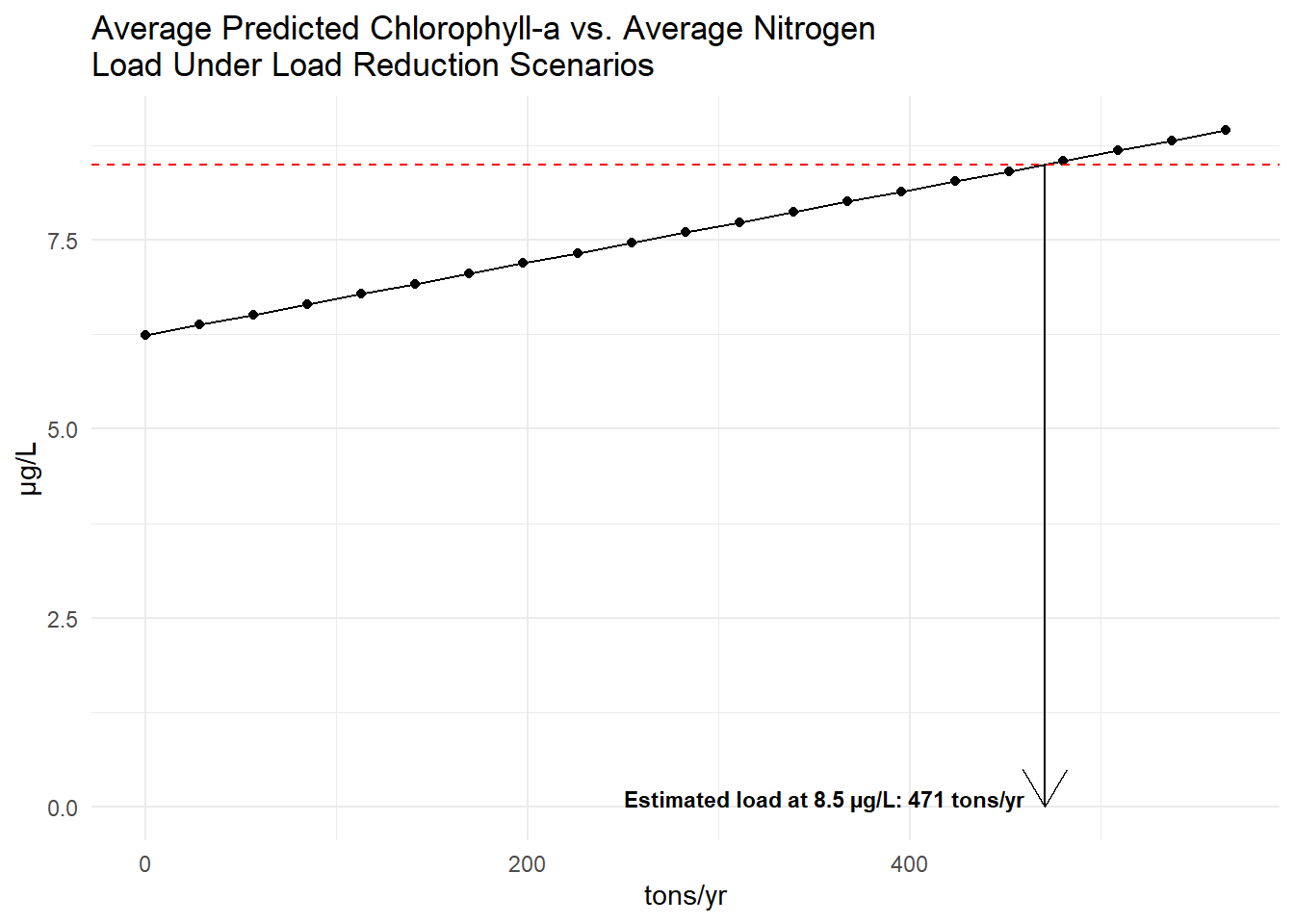
The average response of chlorophyll-a to nitrogen load changes was then estimated by taking the average of the annual chlorophyll predictions and the average load estimates for each reduction scenario. The plots below show each point as the average predicted chlorophyll-a versus the average total nitrogen load for each load reduction scenario. The dashed red line indicates the target chlorophyll-a concentration of 8.5 µg/L. The arrow indicates the estimated nitrogen load reductions needed to achieve the target chlorophyll-a concentration based on linear interpolation of the average response curves. The estimated loads needed to achieve 8.5 µg/L chlorophyll-a are 471 tons/year.
Log-models with additional predictors
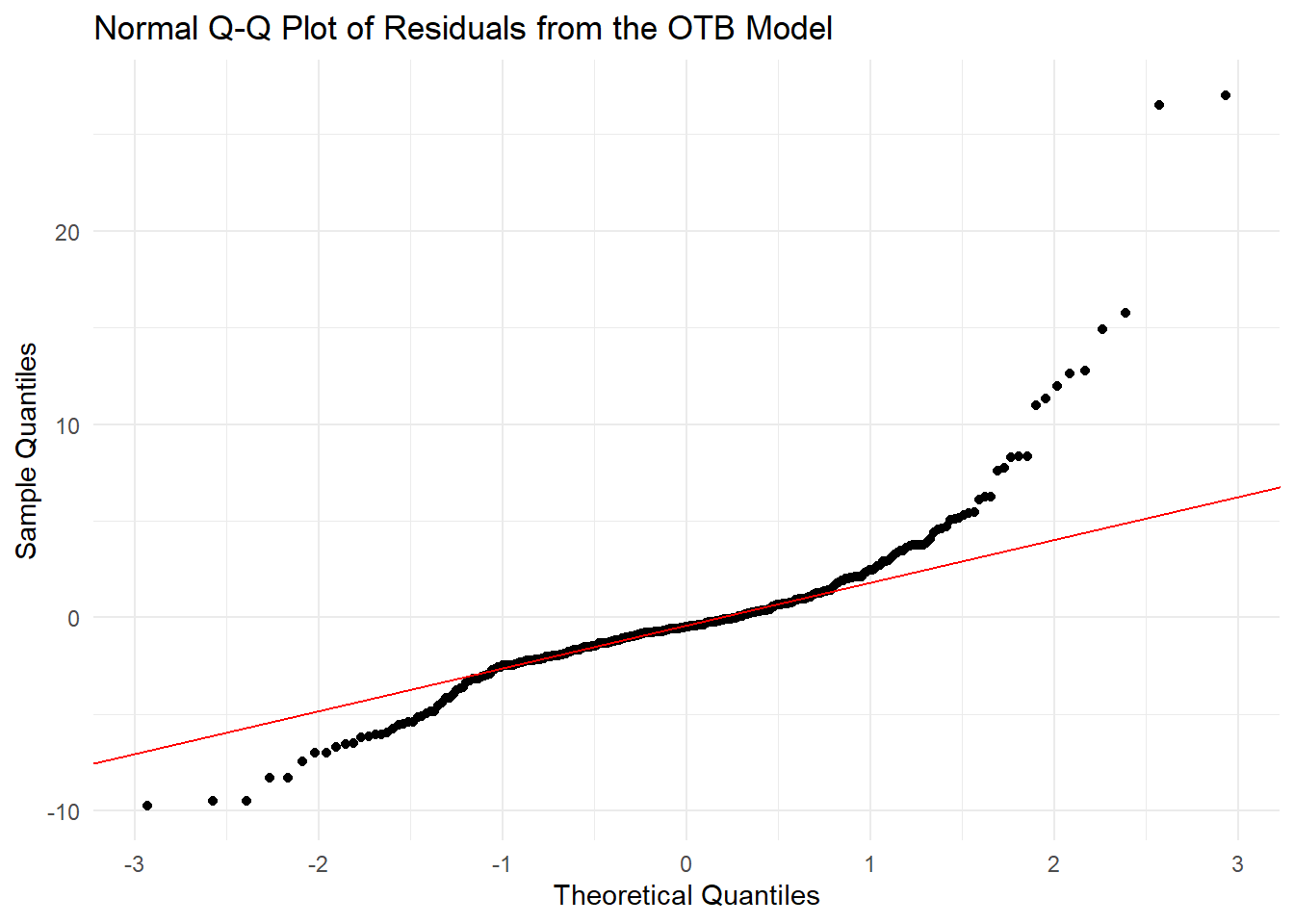
The above models used to predict the assimilative capacity of Old Tampa Bay, particularly for the period after 2010, likely provide an overestimate of how much loading the bay segment can assimilate. This is evident by evaluating the residual patterns - the model does not capture extreme values. Results could be improved by modeling an inherently log-normal response variable and including additional predictors to provide a more accurate estimate of how nitrogen load influences chlorophyll-a.
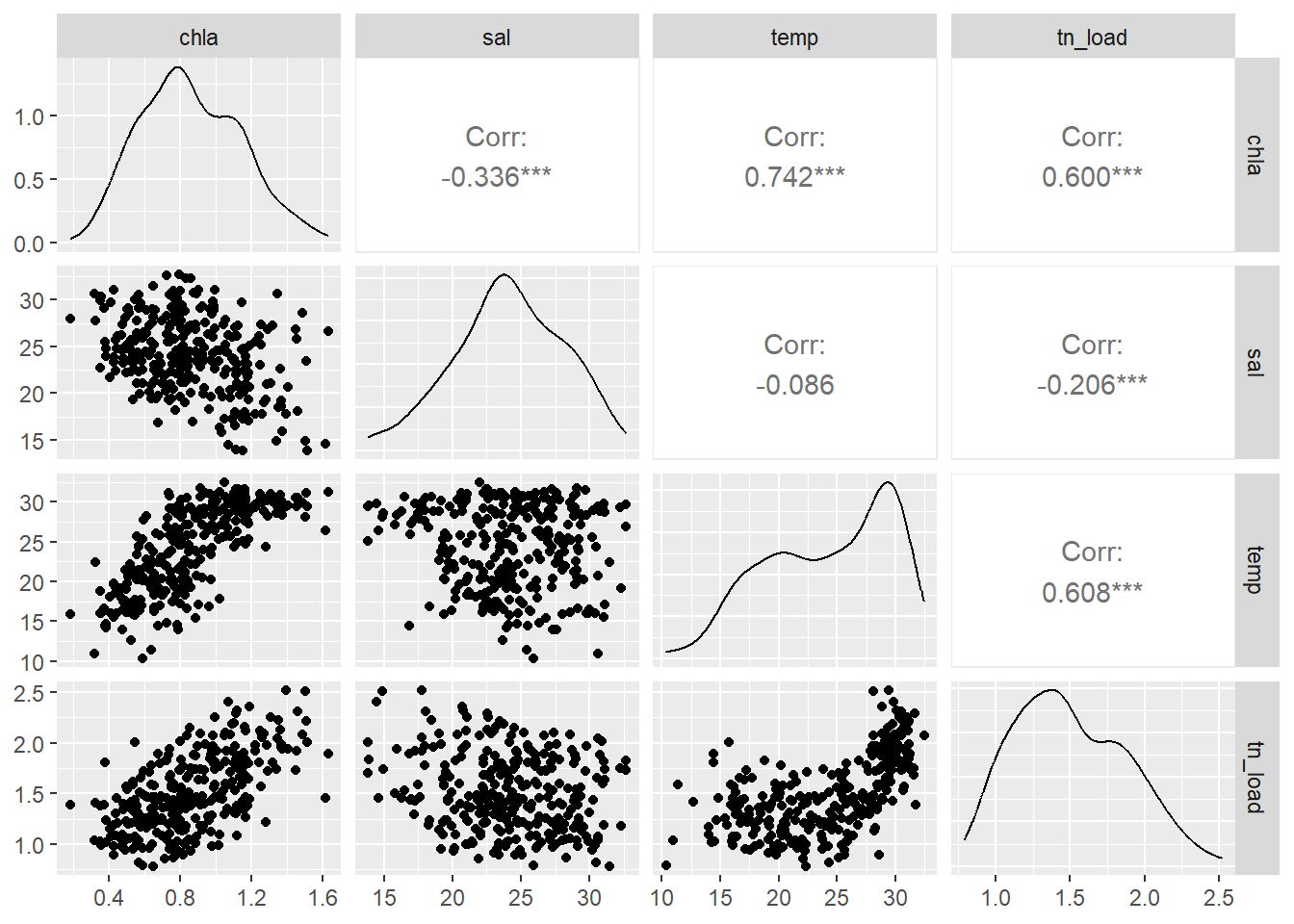
To address this issue, an additional model was developed using log-transformed chlorophyll-a as the response variable and additional predictors, including salinity and temperature.
Collinearity among the new predictors was assessed using variance inflation factors (VIFs), where chlorophyll and load are log-transformed. The values are sufficiently low to include all predictors in the model.
sal temp tn_load
1.046733 1.589310 1.647133 The above analyses were repeated with the following changes to the model structure:
\[ log_{10}\text{chla}_{t} = \alpha_{t} + \beta_1 log_{10}\left( \Sigma_{i = I_0}^{I_n} L_{t - i} \right) + \beta_2 \text{sal}_{t} + \beta_3 \text{temp}_{t} \]
where the coefficients \(\beta_2\) and \(\beta_3\) represent the influence of salinity and temperature on chlorophyll-a concentrations. Chlorophyll is modelled using a log-normal distribution to better capture extreme values and loading is also log-transformed. Below shows the explained deviance (pseudo-r-squared) for each cumulative lag model.
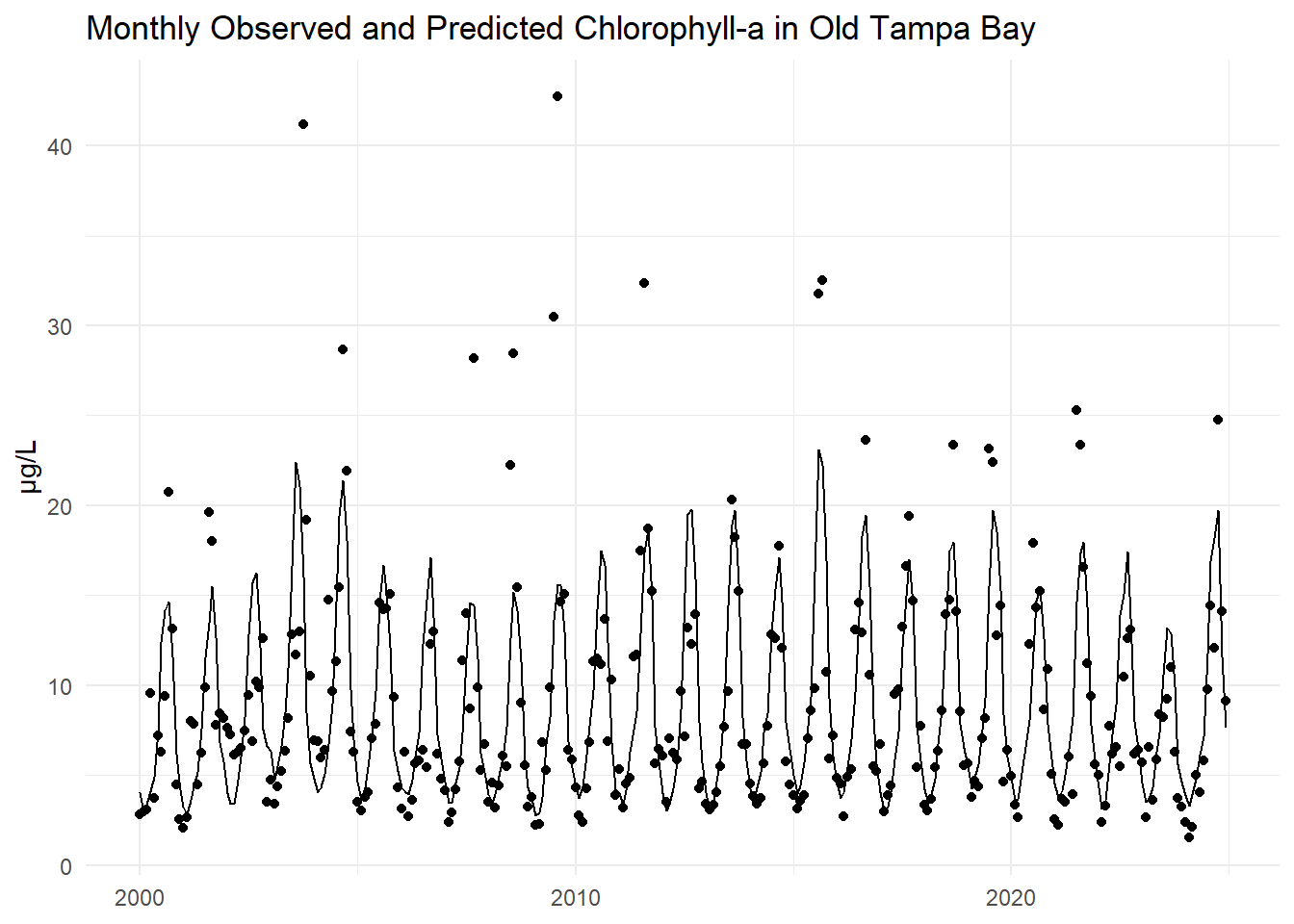
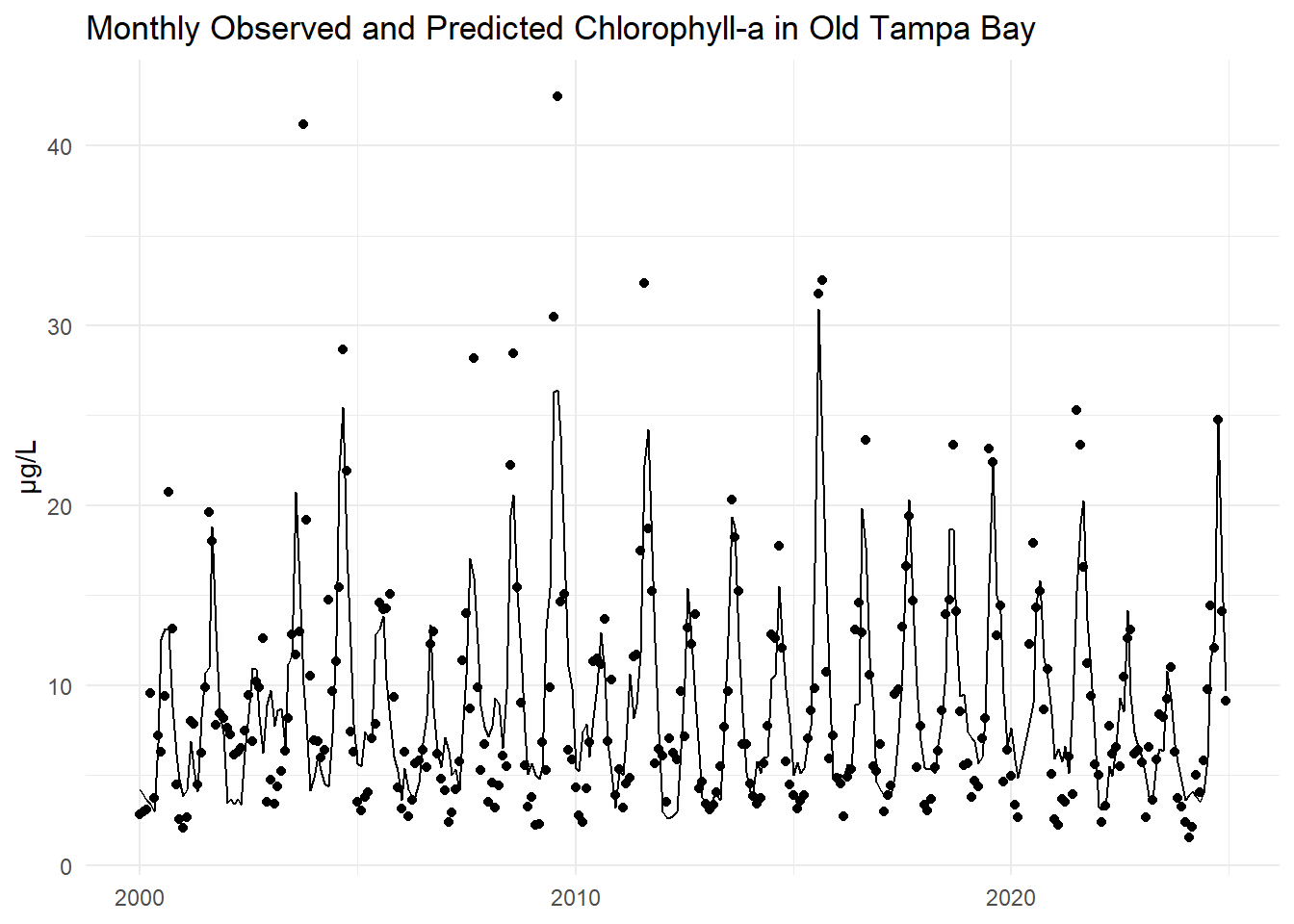
The monthly observed and predicted chlorophyll-a concentrations are compared for Old Tampa Bay below.
The annual average observed and predicted chlorophyll-a concentrations are compared for Old Tampa Bay below.
Monthly and annual model predictions are then generated for various nitrogen load reduction scenarios using the new log-model with additional predictors. Monthly loads are reduced by fractions ranging from 0% to 100% in 5% increments. The models are then used to predict chlorophyll-a concentrations under each load reduction scenario. Salinity and temperature are held constant at their monthly average values for each month across the entire time series.
Monthly model predictions are then aggregated to annual average predicted chlorophyll-a and total nitrogen loads for each load reduction scenario.
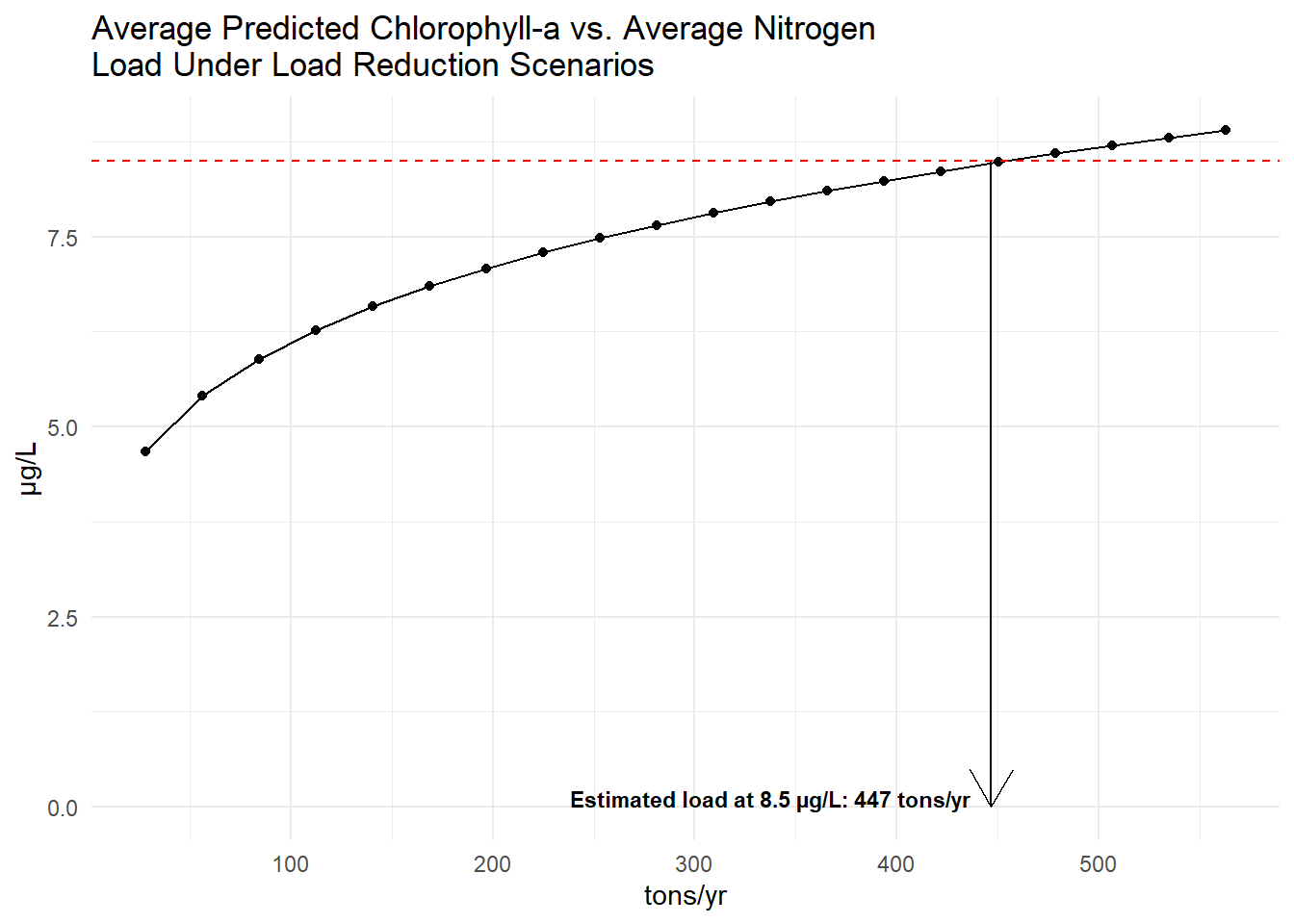
From the load reduction scenarios, the average response of chlorophyll-a to nitrogen load changes was then estimated by taking the average of the annual chlorophyll predictions and the average load estimates for each reduction scenario. The plots below show each point as the average predicted chlorophyll-a versus the average total nitrogen load for each load reduction scenario. The dashed red line indicates the target chlorophyll-a concentration of 8.5 µg/L. The arrow indicates the estimated nitrogen load reductions needed to achieve the target chlorophyll-a concentration based on linear interpolation of the average response curves. The estimated loads needed to achieve 8.5 µg/L chlorophyll-a are 447 tons/year.
Load response by year
A final model structure was evaluated that let the load response vary by year. Only year and load were used as the predictors (month was removed).
\[ \text{chla}_{t} = \beta_1 \left( \Sigma_{i = I_0}^{I_n} L_{t - i} \right) + \beta_2 year_v \left( \Sigma_{i = I_0}^{I_n} L_{t - i} \right) \]
where \(year_v \left( \Sigma_{i = I_0}^{I_n} L_{t - i} \right)\) is an interaction term between year (as a factor) and the cumulative load evaluated at different lags from \(I_0\) for the present month to \(I_n\) months.
The monthly observed and predicted chlorophyll-a concentrations are compared for Old Tampa Bay below.
The annual average observed and predicted chlorophyll-a concentrations are compared for Old Tampa Bay below.
Monthly and annual model predictions are then generated for various nitrogen load reduction scenarios using the new log-model with additional predictors. Monthly loads are reduced by fractions ranging from 0% to 100% in 5% increments. The models are then used to predict chlorophyll-a concentrations under each load reduction scenario.
Monthly model predictions are then aggregated to annual average predicted chlorophyll-a and total nitrogen loads for each load reduction scenario.
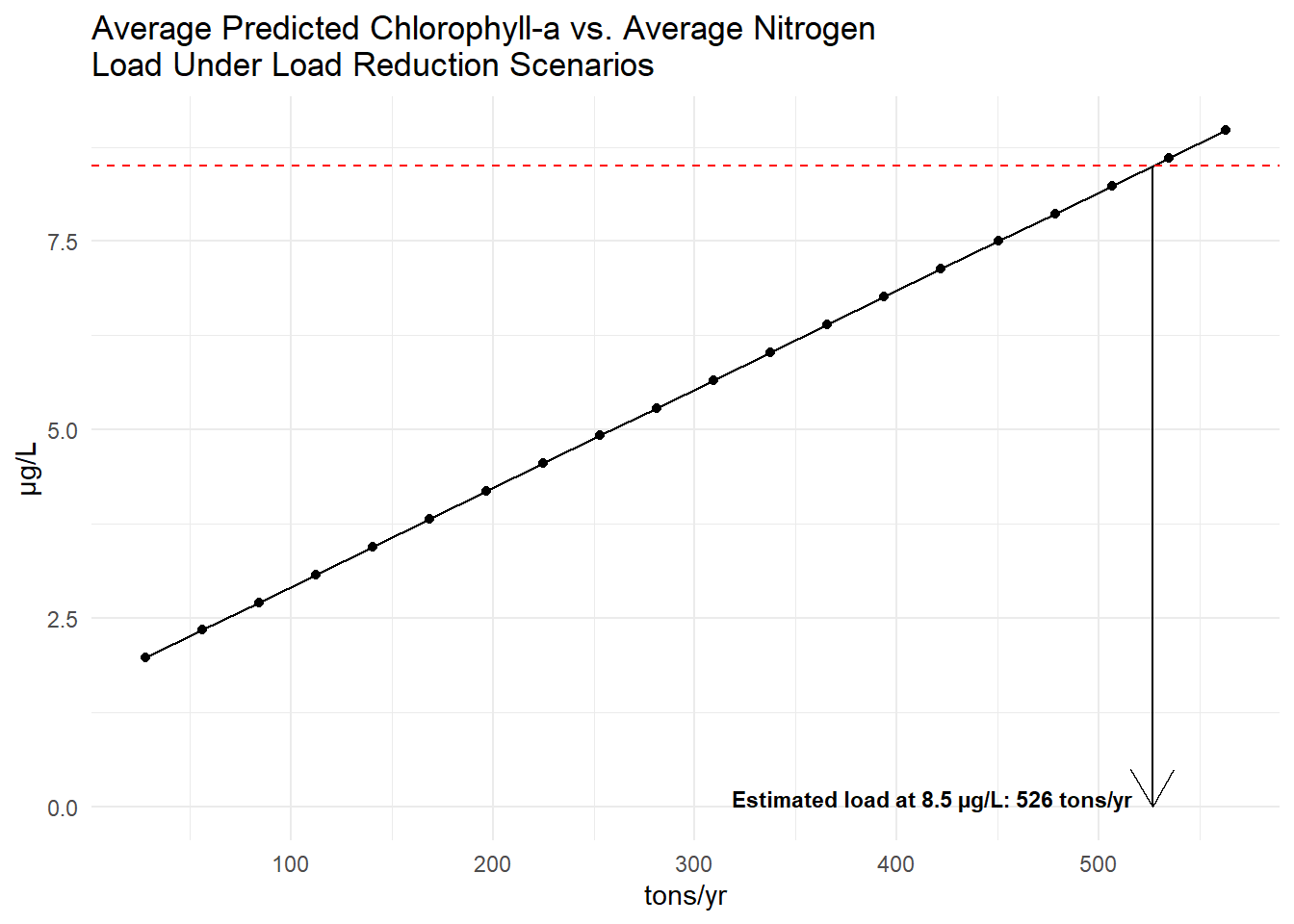
From the load reduction scenarios, the average response of chlorophyll-a to nitrogen load changes was then estimated by taking the average of the annual chlorophyll predictions and the average load estimates for each reduction scenario. The plots below show each point as the average predicted chlorophyll-a versus the average total nitrogen load for each load reduction scenario. The dashed red line indicates the target chlorophyll-a concentration of 8.5 µg/L. The arrow indicates the estimated nitrogen load reductions needed to achieve the target chlorophyll-a concentration based on linear interpolation of the average response curves. The estimated loads needed to achieve 8.5 µg/L chlorophyll-a are 526 tons/year.